Refining the Questions

Testing Concepts and Developing Scales

Most theories involve ‘concepts’ which summarise a range of ‘behaviours’. For example, we may refer to someone as ‘authoritarian’. We cannot see ‘authoritarianism’ as such, but the word stands for a whole range of ways in which the person may respond to a variety of situations. In order to test whether a person is ‘authoritarian’ in their attitudes or in their behaviour, we would need to prepare a range of questions, to ask that person how they responded, how they have behaved, or what were their attitudes.

In the study of religion, there are many ‘concepts’ which one may wish to explore or measure in some way. For example, one might wish to explore how ‘involved’ people were in church life. No one measure will give us an adequate indication. Attendance on Sundays may be one indicator, yet there are many who attend every week who are not very involved in other ways, such as in administration, or in other groups that meet. It is better to prepare a scale which would cover the various ways in which people might be involved, including:

1. Attendance at services
2. Attendance at other activities of the church, such as small groups
3. Undertaking positions of responsibility within the organisation of the church
4. Involvement in decision making
5. Involved in small jobs around the church (apart from specific positions of responsibility).

The scale enables us to add people’s responses to each of these questions, and assess more accurately how involved people are.

In order to develop a scale, it is necessary to:

1. Develop the definition of the concept, in terms of the sort of behaviour or attitudes we wish to measure.
2. Develop questions which cover all the types of behaviour or attitudes covered by the definition.
3. Test the questions, if possible, with a group of people, to see if they do ‘pick out’ the group of people you want to identify.

In many areas of survey work, it is best to use a series of questions rather than rely on the answers to one question. A single question

• may be read incorrectly and thus answered incorrectly;
• may ‘pick up’ an exception to the rule. (For example, a question about attendance at church on Sunday may not measure that people are involved in church life at all. They may go to church each Sunday because they feel obliged to take a relative, not because they have any interest in attending at all.)
• may be answered in terms of a response ‘set’. Sometimes people will just say ‘yes’ all the way through without reading the question properly.

However, if the same question is asked too often, it can cause boredom or annoyance. It is generally important to keep questionnaires as short as possible to ensure that people do, in fact, answer the questions.

Over the years, many scales have been developed which are widely used in research. These scales may cover aspects of personality, belief, attitudes, experiences, and other factors people may wish to measure. It is often helpful to use pre-existing scales in order to ensure that there is comparability with other research. Journal articles may be a useful source of such scales. Another source is the book by Peter C. Hill and Ralph W. Hood, Measures of Religiosity, Birmingham, Alabama: Religious Education Press, 1999, which provides details of more than hundred scales related to religious factors.

There are statistical test specifically designed to check the reliability of scales. This test is included in SIMSTAT and is accessible through the Statistics | Scale Testing | Reliability menu. Having entered the various items that one considers might make a valid scale in one’s questionnaire data, the test produces a range of statistics. The key figure is Cronbach’s alpha. An alpha of more than .7 is generally considered to be indicative of a good scale and a an alpha of more than .8 is considered excellent. Another table that is produced provides an indication of how each item contributes to the scale. Items which are seen not be contributing can be excluded from the scale.

Designing a Questionnaire

In most surveys, there are four groups of questions:

1. Questions measuring the dependent variables – what we actually want to know, or want to measure (such as questions about how people became Christians).
2. Questions measuring independent variables – those factors which might relate to the dependent variable and help to ‘explain’ it (such as the Christian attitudes of parents).
3. Questions about background – such as age, sex, education, occupation, marital status, whether born in the city or the country, ethnic background. These questions help us to look at subgroups of people (such as young as compared with older people) and compare their responses.
4. Questions measuring intervening variables – those factors which are not part of the hypotheses, but which may have an impact on the relationship between the dependent and independent variable and for which one may wish to control.

Look first at the questions other people have designed before writing your own. If you use the questions that other people have used, then you have the advantage of using their expertise and experience. The other advantage is that you may then have data which you can compare with your own. The exact way that questions are worded makes a significant difference to ways people answer the questions.

Many factors are not directly measurable. One cannot measure directly whether the person has an authoritarian character, or whether they hold a particular style of Christian beliefs. In many instances, it is necessary to identify some indicators of such factors which can be measured using scales. For discussion on the development of scales, see the section on refining the questions.

The question about religious denomination, for example, in the Australian National Population and Housing Census has been changed in its form several times over the years. Each time there is a change in the form, the results are affected in quite significant ways. In 1991, for example, for the first time the Census paper provided several boxes to be ticked for the each of the religious groups with which 1% or more of the population had identified at the last Census. People identifying with smaller groups had to write in the name of their religious group. The result was that every group listed increased in numbers, while most of the groups which had to be written decreased. For example, the number of Baptists increased, while the Churches of Christ decreased. The Churches of Christ argued that some of their members ticked ‘Baptist’ as the closest denomination in the list, rather than write in ‘Churches of Christ’.

However, in many instances, the form of the questions used in the Census has been given a lot of thought. If asking for similar information, it is worth looking up how the Census has asked the question. Details of questions are provided in publications available from the Australian Bureau of Statistics (www.abs.gov.au). The Census Guide is a free CD-Rom which provides details of the 2001 Census, of the questions used and the categories of responses, and how to obtain Census data.

Look also at the code-books of other surveys. You will find a few of the questions used in the National Church Life Survey and in the Australian Community Survey on this CD-Rom. Codebooks for other surveys such as the National Social Science Surveys available from the Social Science Data Archives (ssda.anu.edu.au). See also websites such as ‘The Question Bank’: http://qb.soc.surrey.ac.uk. A very useful source of questionnaire scales is the book, Peter C. Hill and Ralph W. Hood, Measures of Religiosity, Religious Education Press, Birmingham, Alabama, 1999.

If you are writing your own questions, it is helpful to keep in mind the following rules:

1. Keep questions simple.
2. Keep them short.
3. The question should only ask one thing at a time.
4. The question should not suggest a particular answer is right.
5. Avoid negative questions.
6. Ask questions to which the person will know the answer.
7. Use words which will have the same meaning for everyone, regardless of background.
8. Ensure the frame of reference is clear. (Ask about what people did ‘last month’ rather than ‘recently’ and about ‘the last twelve months’ rather than ‘last year’ which may refer to the last calendar year or the last twelve months.)
9. The question should be as direct as possible while remaining polite.

There are two types of questions: open-ended (where people write in their response) and forced-choice (where people choose between a range of responses offered to them).

Advantages of open-ended questions:

1. They allow people to write in a full response to the question.
2. They do not restrict people to a pre-determined range of responses.
3. They allow people to make qualifications to their answers.
4. They help people to think that the researcher is really listening to exactly what they think.

Advantages of forced-choice questions:

1. They are answered quickly by the person filling in a questionnaire.
2. They help people who are slow to put their ideas together.
3. They are much easier for the researcher to code and to analyse.
4. They allow people to ‘code’ themselves rather than the researcher doing it.

In surveys, it is best to ask mainly forced-choice questions rather than allowing people to write in their own answers. If people write in their own answers, these must be coded, and this takes an enormous amount of time for the person analysing the questions. It is usually not possible, because of time, cost and accuracy to use many open-ended questions.

Types of Forced-Choice Response Formats

1. Likert-scale. These questions go beyond simply asking people whether they agree or disagree by asking how strongly they feel about their responses. The additional information is often very helpful. The responses from such questions would be considered to be ‘ordinal’ data. There is a definite order in the responses, but one does not know the ‘size of the gap’ for different people between the responses. Provide a statement, and then ask respondents whether they … Agree strongly – Agree – Don’t know – Disagree – Disagree strongly.
2. Ask people to choose between two words at the ends of a continuum. There is a trend in survey design to move towards questions which ask people to score on a scale of 0 to 10. Most people are familiar with such scores. They know that 50 or more is ‘a pass’ and that 80 or above is ‘a good score’. Most people find such scales easy to use. At the same time, dividing people’s responses into eleven options means that while the gap between their scores remains subjective, it is not as likely to be as different as if people were asked to score from 0 to 4. Most researchers are willing to treat scores on a scale as interval data despite the fact that they only approximate intervals because of the subjective element, rather than as ordinal data. As interval data, the possibilities for analysis are more numerous and richer. For further information about the various types of data: nominal, ordinal and interval, see the sections on analysis, particularly Univariate Analysis. For example, we might ask people to indicate how they felt about church life.  Discouraged 0.1 . 2 . 3 . 4 . 5 . 6 . 7 . 8 . 9 . 10 Enthusiastic
3. Ask people to choose between a range of alternatives. This provides categorical or nominal data. The list can be presented in any order. The numbers which are recorded refer to specific categories or ‘names’ which cannot be naturally added together or averaged. It may be possible to re-categorise, however. One could have a category of those people who have been married but who currently are no longer married, which contained ‘divorced’ and ‘widowed’, and, depending on how one defined the ‘no longer married’ , those who said they were ‘separated’. Care should be taken to ensure that one presents categories only of one kind within the question to avoid confusion. If one added to the list ‘in a de facto’ relationship, how would the person respond who was both ‘married’, ‘separated’ and ‘in a de facto relationship’. Because of this problem the Australian Census has chosen to ask about ‘registered marital status’ and ‘living arrangements within the household’ in separate questions. Are you …
   1. Married
   2. Never married
   3. Separated
   4. Divorced
   5. Widowed (In these types of questions, we must make sure we have a full range of possible responses, or we must add an extra category …
   6. Other (please explain) ………………………………
4. Ask people to choose from a list of possibilities. For example, circle each of the positions you currently hold in the church. 1. Minister 2. Secretary 3. Treasurer 4. Organist 5. Coordinator of evangelism 6. Coordinator of pastoral visitation 7. Sunday School superintendent 8. Sunday School teacher. (In this case, it would be quite possible for people to hold more than once position.)
5. . Ask people to rank a list of answers in order of importance. For example, how important are the following functions of the church? Put ‘1’ beside the most important, ‘2’ beside the next most important, through to ‘5’ for the least important. These questions are popular in that they can provide some interesting and detailed information. However, they are difficult to analyse statistically and quite difficult for people to answer, particularly if the list of options to be ranked is a long list. While it may be relatively easy for people to identify the most important and the least important, putting all the other responses in order may be difficult. Indeed, if people are forced to make choices they would not readily wish to make, their responses may not be very meaningful. An alternative way of obtaining similar information is to ask people to evaluate the importance of each of the following on a scale, say of 0 to 10. This means that they only have to consider one statement at a time. To provide an additional ‘check’ one can then ask people to indicate which of the list of items they consider MOST important. …. Providing charity for the poor …. Worshipping God through regular Sunday services …. Evangelising people who do not attend church …. Seeking to change the whole society in which we live …. Providing good hospitals

 Ordering of Questions

Here are some guidelines adapted from a book entitled Surveys in Social Research by David de Vaus (2002) for the ordering of questions in a survey.

1. Commence with questions the respondent will enjoy answering. Such as A. Easy to answer questions
   B. Factual questions (such as questions about behaviour)
   C. Not background questions such as those about age, education.
2. Go from easy questions to more difficult questions and concrete questions (about behaviour) to abstract questions (about how a person thinks).
3. Group questions into sections so that people can understand the flow of the questions and see the point of what they are doing.
4. Use filter questions, if applicable, so that when you require information only of a few people, other people do not have to answer that question. However, use filters sparingly because they often confuse people and people are often not sure when they should start answering again.
5. When developing scales, use a mixture of positive and negative questions to avoid people scoring the questions all one way without thinking thoroughly about their answers.
6. Try to keep the questionnaire interesting. Make the questions as interesting as possible. Use a variety of formats for answering.
7. Demographic questions, which are usually answered easily, are often best placed at the end of the questionnaire or in natural contexts within the body of the questionnaire, but not as a group. For example, there may be a set of questions on family life in which the question about marital status could be asked or questions on work in which one could request the person’s occupation.
8. When people are choosing between options, it is usually helpful to give them the option of ‘Don’t know’ or ‘Other (please explain)’ so they feel they are not forced to make choices they do not wish to make.

References:

De Vaus, David, (2002), Surveys in Social Research, 5th edition, Sydney: Allen & Unwin.

Hill, Peter C. and Ralph W. Hood, (1999), Measures of Religiosity, Birmingham, Alabama: Religious Education Press,

Selecting a Sample

The advantage of using a questionnaire is that it is possible to get information about a whole group or information which can be generalised to a wider group of people. If so, one must be careful about when and to whom the questionnaire is given. This involves the issue of ‘sampling’. (See below.)

It is usually important to have a high ‘return rate’. In other words, most people asked to complete the questionnaire actually do complete it. There are many ways of ensuring a high ‘return rate’. For church attenders, it is usually best to ask people to fill it in at church rather than take it home and bring it back another time (which many people will forget to do).

Population

The ‘population’ is the group of people one wishes to study and about whom one wishes to make comments. For example, if one wanted to say something about Internet users in Australia, then the population is all those people living in Australia who use the Internet. We may want to restrict our definition of the population to all people who use the Internet at home, or all people who use it other than for work purposes. Or the population one wishes to study may be those who attend a particular church or who reside in a particular suburb.

Note that it is not always easy to identify the appropriate population. If we were interested in how people feel about church worship services, we will want to include in our study why some have left, and will thus want to include people who used to attend church as well as those who currently do so. When we listen to the people in the congregations, we will listen only part of the ‘population’ in which we are interested. They are also a biased part, for these are the people who have responded positively to what has been offered. We cannot generalise from ‘church attenders’ to a wider population.

In developing a project and in writing it up, we must clear about the population we are actually examining. For example, suppose a survey is posted to a random selection of Australians, but the survey is only in English. By the very design of the survey, the population able to respond is people who can read and write in English. Thus, that part of the population unable to do that is excluded by the design. It is very likely that those who cannot read and write English, and for that matter, those who do not have a postal address, will have quite different opinions on a range of issues from those who are familiar with English. Some will be indigenous people. Others will be recent Asian immigrants, for example. The fact that such groups were excluded by our design from our population should be made clear in writing up our results.

Sampling

Sometimes, within a church situation, everyone can be asked the same questions. In most circumstances, this will not be possible. However, we will want to know that those members of the targeted population who filled in the questionnaire represented the opinions of those people who did not fill it in. To do this, it is important to sample properly.

There are two major ways of sampling.

1. Random sampling means that the people who fill in the questionnaire are chosen randomly from the total targeted population. This is usually done by obtaining a list of everyone, and then picking people at random from the list, usually with the help of a ‘random number generator’. A random number table as has been included on this CD-Rom can be used for this purpose.
2. Stratified sampling means that various subgroups of people are carefully chosen from the total group to ensure that an appropriate range of people are represented. Thus, one may choose some young people and some older people, some well-educated and some not so well-educated if age and education are two of the factors which appear in the hypotheses. This is generally not such a reliable method, however, for it is not easy to know in advance all the factors which may be important to the survey and in which subgroups one might be interested. However, there are occasions, particularly when examining small sub-groups that some sort of stratified sampling is important to make sure those groups are adequately represented.

For example, in the Australian community survey, the researchers wished to compare the community life of people who lived in sparsely populated areas with people who lived in more rural and urban cities. There are comparatively few people living in sparsely populated areas. Hence a random survey of Australians would not provide sufficient of these people to draw any conclusions about them.

To ensure there were sufficient numbers in the sample, all Australian postcodes were divided into eight groups: four groups of urban postcodes, distinguished by socio-economic level and four groups of rural postcodes distinguished by the size of the population in each of them. A similar sized group of people was drawn randomly from each of these eight groups of households using the lists of people on electoral rolls. Thus stratified sampling and random sampling were both used in the drawing of the sample. The questionnaire was sent to approximately 2000 people in rural areas where there was no centre of population larger than 200 people and to 2000 people in high socio-economic areas in the State capital cities and to each of the other types of areas identified.

The result was that a sample of more than 1000 responses was obtained from people living in sparsely populated rural areas as well as a sample of 1000 responses from people living in high socio-economic city areas. Conclusions could be drawn about community life in each of the eight areas.

Because all Australian postcodes appeared in the original sample thus covering the total population of Australia, and because the Census provided information about the numbers of people living in each of these groups of postcodes, it was possible to weight the information in such a way to also provide a representative sample of the total Australian population.

Size of Sample

The larger the sample, the more accurate are likely to be the results in reflecting the opinions of the total population. However, the relationship between sample size and accuracy is not linear and is related more closely to the actual numbers of the sample than to the percentage that the sample represents of the total group.

The following table represents the ‘sampling error’ for samples of different sizes:

Sample Size	Sampling Error at 95% Confidence Level
100	10.0%
156	8.0%
204	7.0%
400	5.0%
625	4.0%
1100	3.0%
2500	2.0%
10000	1.0%

What this table provides is the size of the difference we would might expect between the responses of the sample and the responses of the total population which is being examined. For example, supposing we were looking at what proportion of the population attends church services in a twelve month period. If we ask just 100 people, we can be 95% sure that the true figure is within 20% (10% either way) of the figure we have actually found from our sample. Thus, if 33% of that group says they attend at least once a year, then we can confident that the true figure lies somewhere between 23% and 43%. If we ask 1100 people that question, we can be confident that the true figure is within 6% (or 3% either way) of the figure that we discover.

In most surveys, people are satisfied with the accuracy obtained from 2500 randomly chosen people, or even a sample of 1100. However, smaller samples are unlikely to provide usable accuracy for most purposes. Thus, it does not matter if one is interested in the attenders of the Uniting Church in the State of Victoria, or in the total population of Australia, a sample of at least 1100 is desirable. Only in instances where the sample is quite small such as the congregation of a particular church, or all ministers of Pentecostal churches, is the sample size required much different. In these circumstances, it is advisable to head for a high percentage of people.

It should be noted that when one is looking at particular groups within the sample, their size is what determines the sampling error. Thus, in a sample of 1100, one is likely to have around 550 males and 550 females. Thus, the sampling error of the male or female sub-groups will be around 4.6%, rather than 3%. If one is looking at the group of people who are in their 20s, the sampling error may be closer to 7%. Hence it is important to have a sample of sufficient size for each of the major sub-groups for which one wishes to draw conclusions.

The sampling error is dependent largely on the numbers of the groups from which one draws the sample. If one randomly chose churches and then asked everyone in those churches to complete a questionnaire, even though one may have thousands of surveys, the random error would be closer to the number of churches than the number of returned surveys. The fact is that people in one church are likely to be different from people in another. Thus, it is much better to have a few people chosen randomly from a large number of churches than a large number of people responding from a small number of churches. It is important to maximise the numbers of units from which the sample will be drawn.

Response Rate

Another factor to take into account in the sample size is the response rate that may be expected. Not everyone will fill in the questionnaire. The sampling error depends on the actual numbers that are returned, not the numbers of questionnaires distributed. Further, a low percentage returned increases the sampling error. Thus, if one only has 50% of surveys returned, one’s level of confidence will not be as high as if 75% were returned.

It is common in National questionnaires to receive back only 50% of surveys or less. There are usually specific biases among those who respond compared with those who do not. People with higher levels of education are more likely to respond. Those who struggle with reading and writing are not likely to respond at all. People whose first language is the language in which the questionnaire was written are more likely to respond than those for whom it is their second or third language. The percentage returned depends partly on the interest and personal investment that people have in the topic being examined. People who attend are far more likely to complete a questionnaire about church life than people who do not attend. Even among church attenders, it is more likely that the people at the core of the church life will complete a questionnaire given out in church than those people who are on the fringes or who are visiting.

In some cases, market researchers work with response rates of less than 20%, and thus their results have a very low level of accuracy. They are often dealing with people who have little or no loyalty to the company or products and are reluctant to assist.

One can improve the response rate in several ways, such as by

• sending a preliminary letter explaining the survey and how important it is
• making the questionnaire short and easy to answer
• providing some reward for those who complete the questionnaire (as long as anonymity can still be retained)
• sending a gift with the questionnaire (All sorts of gifts have been tried such as tea bags, raffle tickets, and so on. It is the good-will expressed by the gift which is probably more important than the gift itself.)
• sending reminder letters, politely worded, sent at good intervals and drawing attention to the importance of the survey. More than three letters is probably counter-productive however.

In choosing a sample, it is wise to build the return rate into one’s plans. Thus, if one wants 1100 questionnaires to be returned, it may be wise to send out at least 2500.

Evaluating the Sampling of Others

When evaluating the research of others, as reported in books and journals, it is important to examine the details of the sampling that has occurred. Look at the size of the sample, and the ways in which the sample was drawn. Was it truly a random sample? Are there likely to be systematic biases built into the sample, such as through the languages used, or built into the original list from which the sample was drawn? Is the researcher drawing conclusions about small sub-groups of the sample? What does the researcher say about the response rate? Are there likely to be differences between those who responded and those who did not respond?

Pilot Testing

A questionnaire should be tested thoroughly before it is used. It may be helpful in the first instance to ‘talk’ the questionnaire through with someone who can look at it critically and who can point out ambiguities, questions which are not clear, lists of responses which are not complete, and areas in the questionnaire where the questions do not flow easily.

Then the questionnaire should be given to a group of people who are similar in their background to those with whom the questionnaire will be finally used. If the questionnaire will be used with a variety of people, such as people of different ages, check it with a similar range of people.

When doing a pilot test, check the following.

1. Everyone can understand the questions. Ask people in the pilot questionnaire to make any questions they cannot understand or feel are ambiguous.
2. People can answer the questions. Check that most people do answer the question, and that there are not many ‘Other’ or ‘Don’t know’ responses. Also check that there are a range of responses, which will show that the questions are distinguishing between different groups of people.
3. The scales work. If you have developed scales, you can check at this stage if they work, and people who are answering one question in the way you expect are generally answering the other questions in a similar way.
4. The questions do not encourage a ‘response set’. That people are not responding to a set of questions all in the same way, regardless of the content of the question.
5. Is there a good spread of responses to questions? If everyone is answering a question is the same way, the question is not distinguishing between different groups of people. It may be more useful to ask something similar which will provide a greater spread of responses. For example, ‘Is it right to cheat on your partner?’ (Yes / no) may be replaced by the question ‘Are there any occasions on which extra-marital sexual activities may be justified? (Absolutely never, almost never, sometimes, often.)
6. The time involved in completing the questionnaire. Generally, the less demanded a task is, the more people will actually do it. However, the more important factor is whether people feel that their contribution is worthwhile. If they feel that they are doing something which makes a real contribution, they are more likely to do it even if it does involve some time.
7. Add a few questions at the end of the pilot about the questionnaire itself. Did people find it easy to follow and easy to answer? How long did it take them to answer the questions?

Conducting a Survey

Prior to conducting a survey:

1. The questionnaire has been written and prepared for distribution
2. The sample has been drawn
3. Permission to proceed has been obtained from an ethics committee.

The questionnaires are sent or delivered to the various people in the sample, making sure that each person drawn in the sample receives one. Again, it is likely that if one is obtaining information from people in a congregation that those members of the congregation who are not attendance will have different ideas from those who are in attendance on a typical Sunday. Thus, if one wants to make comments about the members of the congregation, take the trouble to send questionnaires to those who are not in attendance when others are distributed.

The questionnaire should contain an introduction which explains:

• the purpose of the research
• who is conducting it and who has auspised it
• that completing the questionnaire is voluntary
• how results will be used
• how confidentiality will be maintained
• how to obtain further information about the research
• how to make a comment or complaint to the ethics committee
• how the questionnaire is to be returned.

It is also usual to provide some examples of how to complete the questions in the questionnaire and clear instructions as to whether to tick boxes, cross them, circle numbers of whatever is the required form of completion.

To preserve anonymity, it will be necessary to provide a way of returning the questionnaires so that the person completing it cannot be identified. A ‘Reply Paid’ system can be set up with the Post Office. Or stamped and addressed envelopes can be provided. The researcher should not expect that the person completing the questionnaire should carry the burden of the cost of returning it.

A good response rate is crucial for drawing valid conclusions. In order to encourage people to complete the questionnaire, it may be necessary to remind them, perhaps with a letter and perhaps an additional survey form in it. There is a small dilemma here. Does one put an identifying mark on each survey so that one can cross each person off as they send their survey in? Or does one go down the path of complete anonymity of questionnaires? Identifying marks, however well camaflaged, discourage some people from completing the survey. But not using such marks means that reminder letters must be sent to everyone. Such letters can written thanking those who have responded and encouraging those who have yet to complete it to do so soon.

Give people adequate time before the reminder letter. A period of three weeks from the time they would actually receive the questionnaire is reasonable. A reminder letter can be sent at the of the fourth week giving people another two weeks or so.

Data Entry

Very limited analysis can be done of surveys by hand. Even if one only uses a spreadsheet, it is highly desirable to enter the data into a computer file.

Write on each returned questionnaire an identifying number. This way, one can always check the data that has been entered in the computer file.

The questionnaires need to be coded. In other words, a number must be assigned to each response category. It is usually easier if responses are numbered in the printed questionnaire so that these numbers can easily entered when the data is entered into a computer file. For example, with a question such as:

What is your marital status?

1. Single
2. Married
3. Divorced
4. Widowed

one will enter, for each questionnaire the number 1, 2, 3, 4 – whether the respondents have been asked to tick a box or circle the number.

In questions such as

Australia is good country in which to live.

Strongly agree / Agree / Neutral / Disagree / Strongly disagree

it will be necessary to assign a number to ‘Strongly agree’ and each of the other codes. If one wants to add the responses of several questions about Australia as a place to live, one may choose to give ‘Strongly agree’ a score of +2, and Strongly disagree a score of -2, so that positive responses will add in the same direction and ‘neutral’ responses will add nothing to the scale.

You may choose to develop categories and numbers for responses to questions in which you have given people the chance to write in their own answers. For example, if you asked people’s denomination, and then said ‘Other’, you will need to work out a numerical system for all other denominations added by the respondents.

If you have included open-ended questions, you will need to read through all the responses, categorise their answers, and then develop one or more schemes for numbering each of the categories.

You will also need to work out a code name for each question. Most statistical packages like code names which are no longer than eight characters in length. One way of doing this is to choose a single first letter which will indicate what group the question belongs to, such as ‘D’ for demographics, ‘V’ for value questions, ‘P’ for personality questions, ‘W’ for work questions, and then use a unique key word in the question to indicate the name of the question. This makes it relatively easy to find items in the database. For example:

Dmarital – Demographic question about marital status

Vequal – Question about the value of equality.

Note that if you ask a question in which respondents can make several responses, it is usually necessary to treat each of the possible responses as a separate question in the data entry. For example:

Which of the following positions have you held in the church? (Tick all that apply)

1. Secretary
2. Treasurer
3. Elder
4. Sunday School teacher
5. Musician.

Each position will have its own code name and will be entered separately: eg Csecret, Ctreasur, Celder, CSSteach, Cmusic.

Having created the coding one is ready to enter the data. In Simstat, for example, go to the File menu and enter ‘Data / New’. A dialogue is presented which asks for the code name of the variable (question item), the type (whether it is Character, Real number, Integer, Logical, Date, Memo) variable, the size or number of digits or characters for the variable, the number of decimal points, and then a description – into which one could put the wording of the question or a short description of the variable. Having completed the dialogue box for all the variables, a ‘spreadsheet’ is provided with the variable names or codes across the top. Each questionnaire is then entered in its own row.

If one is using a spreadsheet such as QuattroPro, Excel or Lotus, then enter the data in a similar way: code names for each variable across the top, and each questionnaire as a row in the spreadsheet. In this format, it is easy to transform the data into another format for use in another program. Most statistical programs will read data which has been entered into a spreadsheet in such a form.

Go to the Data menu in Simstat, and go to variable definition. This brings up another dialogue box which allows to modify the display of the data, to add a longer description of the variable, to add missing values, and value labels. It is usual to assign a particular number to questions which have not been completed in the questionnaire (such as -9). If -9 is defined as a missing value in the variable definition, then it will not be entered into analysis. Some people have a different number (such as -8) if two answers have been given to a question where one has been requested. In many forms of analysis, this can only be treated as missing data too. An alternative is to randomly choose from the various answers which have been given which one will be accepted. The value label tab will allow one to add the labels corresponding to the various responses to the question, for example: 2 – Strongly agree, 1 – Agree, 0 – Neutral, -1 – Disagree, -2 Strongly disagree.

Once all the data has been entered, it is worth running frequencies and making sure that the responses for all questions fall within the number of responses that one has for each question. If one begins to find ‘3’ and ‘4’ in the questions where the responses are from +2 to -2, obviously some mistakes have been made. It will be necessary to go back and check the original questionnaire and re-enter that data. When this ‘cleaning’ has been completed, analysis can begin.

Univariate Analysis

The first level of analysis is univariate: one variable at a time. Analysis will usually start by looking at the responses one received to each question. This can be done in a spreadsheet program such as QuattroPro or Excel using built in formulas. It is much easier, and the results much easier to read and analyse in a statistical program such as Simstat.

In Simstat, open your data file. Go Statistics | Descriptives | Frequency. This will bring up a dialogue box. On the right of it is a tab entitled ‘Choose’. Click on this to choose the variables which you wish to examine. The ‘choose’ dialogue asks you to distinguish between ‘independent’ and ‘dependent’ variables. At this stage, this distinction is not relevant. You can put all your variables into the independent box. The distinction will become important in bivariate analysis. It also asks for ‘Integer Weight’. Again, this may not be relevant to your database. If on the other hand, the data has been weighted in order to reflect more accurately the population about which you wish to draw conclusions (as in the example of the Australian Community Survey described in ‘Sampling’), enter the variable which has been created for the weight.

Simstat gives you the option of created some charts at the same time as doing the analysis. The type of chart depends on whether the type of data you are looking at. It is usual to identify three types of data:

• nominal (also referred to as categorial)
• ordinal
• interval (also referred to as continuous).

Questions which ask people for a specific category of information, such as whether they are male or female, what their occupation is, and what religion they identify with, gathers ‘nominal’ data. In nominal data, the responses can be numbered in any order. The particular number assigned to ‘Catholic’ or ‘Anglican’, to ‘married’ or ‘divorced’ is quite arbitary. Hence, adding the numbers, or looking at averages is totally inappropriate. Hence, choose a chart in the nominal section. Such as a bar chart or pie chart.

Ordinal data is a little different in that the numbers do have a definite order about them. There is a specific order between the categories ‘Agree strongly’ to ‘Disagree strongly’, although the exact numbers given are arbitary. One could assign the responses scores of 1 to 5, or -2 to +2, or even assign them scores of 10 to 50. Ordinal data has a definite order built into the nature of the data, but the exact numbers assigned and the distinctions represented by the gaps between the numbers are arbitary. Hence, the difference between ‘strongly agree’ and ‘agree’ may be different for different people, although there will be agreement about the ‘direction’ of the difference. For many purposes, as here, ordinal data should be treated as nominal data.

With interval or continuous data, the numbers assigned are not arbitary but have some correspondence with the real world. Thus, the number assigned to one’s age actually represents the years of life. The number of times one has attended church in the past year can, in theory, be counted by an independent observer. One’s height and weight are continuous data in that they may vary ‘continuously’ over a range.

If you only ask if people are ‘under 40 years of age’, ‘between 40 and 59’ or ‘sixty and over’, then one only has ordinal data. It is best to collect interval data if possible, because interval data can be reduced to ordinal or nominal data, but rarely can ordinal or nominal data be changed into interval data.

The only exception to this are scales. Scales are often developed by adding together several ordinal questions. These scales ‘approach’ interval or continuous data, and may be treated in that way. For example, one might ask people

• How satisfied are you with your income?
• How satisfied are you with your intimate relationships?
• How satisfied are you with your community?
• How satisfied are you with what you have achieved in life?

If each is scored on a range of 0 to 4, the four questions will have a total range of 0 to 16 and may provide some indication of how satisfied people are with life overall. This new variable created by adding the others together could be treated as interval or continuous data. As the number of possible responses increases, the possible difference in meaning that the gap between any two numbers has decreases. Hence, there are mathematical as well as practical reasons for treating such variables as ‘interval’ or continuous data. In such cases, one might ask Simstat to draw a ‘Box and whisker plot’.

Simstat will create the responses in a useful notebook. The charts will be created in a separate ‘folder’ of charts. Simstat automatically creates its own index so that one can find the results that were of interest.

In the Frequency table, for each response category, Simstat will give the number of times that people made that response. It is these numbers of responses which are graphed in a bar chart. In the Frequency Table, there are three columns of percentages:

• Percent – is the percent of that respondents making that particular response out of the total number of respondents.
• Valid percent – leaves out of the calculation all those people who did not answer the question at all.
• Cum response – which may be of interest in ordinal and interval data, provides a cumulate percentage, adding the various responses down the table.

Below this table are a number of statistical figures. What is of interest again depends on the type of data.

With nominal data, the mode will be the only figure of great interest. The ‘mode’ is the most frequent response.

With ordinal data, one may also be the median may also be of some interest, indicating the 50% point – at which 50% of the responses are above and 50% are below. Overall, then, it may tell us for example, if most people are closer to ‘strongly agree’ or to ‘agree’ in their responses to a particular question.

With interval data, one may be interested in the mean (all the scores added together and divided by the number of responses). The standard deviation may also be of interest indicating the extent to which most responses are close to the mean. It is calculated by adding all the differences between each response and the mean, adding them together, dividing by the total number of responses, and then taking the square root of the answer. The smaller the standard deviation, the closer are most responses to the mean. For example, if the questions about satisfaction with various aspects of life were each scored from 0 to 10 and treated as interval data, a smaller standard deviation on satisfaction with income than on satisfaction with one’s achievements would suggest that people vary less in their feelings about income than with achievement. If responses are distributed in a ‘normal curve’ through the population, as most people are between five foot and six foot in height, with just a few people outside of that range, 68% of all responses will lie within one standard deviation above and below the mean. With most responses which are normally distributed, 95% of all responses will lie within two standard deviations from the mean.

The third column of figures, Kurtosis and Skewness, have to do with extent to which the pattern of responses reflects a normal curve. For more details on these statistics, see more detailed books on statistics such as David De Vaus, Analysing Social Science Data, Sage Productions, London, 2002.

Box and whisker plots provide a summary of interval data. The box in the middle of the graph shows the area into which 50% of the responses fit. The lines or whiskers, which usually extend both from the top and bottom of the box, show the area in which most other responses fit. Any responses which are quite different from the remainder of the sample, extending more than 1.5 box-lengths from the edge of the box, are marked with circles as ‘outliers’ and one will find any which exist beyond the end of the whiskers.

Bivariate Analysis

Bivariate analysis involves looking at the relationships between two variables. There are three major ways in which this can be done statistically. The method one chooses depends on the nature of the data.

1. Cross-tabulation can be used with most kinds of data, but is the only form available when both variables are either nominal or ordinal data. It is not so suitable when either of the variables is interval data, although interval data can often be re-coded for form specific groups which can then be used in cross-tabulation. For example, if one asks for people’s age, or year of birth, one can re-code that information into groups such as
   1. 20-39
   2. 40-59
   3. 60 years and over.

The groups created by re-coding can then be used easily in cross-tabulation. It is often useful to create such groups, and then use cross-tabulation to examine interval data because cross-tabulations allow one to see relationships which are not linear. For example, if one was looking at the relationship between age and involvement in voluntary groups, one might find that the relationship with age was not linear: that the middle-aged group has higher levels of involvement than either younger or older people. Such a relationship could be seen either by graphing the data (which generally will show little if one has hundreds of cases) or by using cross-tabulation.

A cross-tabulation is created in SIMSTAT from the ‘Tables’ menu. SIMSTAT asks you choose independent variables – which you consider may have an affect on the dependent variables. Thus, if one thought that age might have an affect on involvement in voluntary groups, one would place AGE in the list of independent variables and the measure of involvement in voluntary groups in the dependent variable list. Several variables may be listed at any one time, and a separate table will be produced for each possible relationship between independent and dependent variables. Thus, if there were three variables in each list, nine cross-tabulations would be produced.

It is important to choose carefully what percentage figures will occur in the table that is produced. Independent variables are placed by SIMSTAT as columns in the table, and the dependent variable is placed in rows. Often, the column percentage will be the most important percentage to examine.

Positive about Church Life?	Anglican	Baptist	Catholic
Strongly Agree	195 (8.8%)	34 (18.8%)	336 (17.1%)
Agree	464 (21.0%)	81 (44.8%)	616 (31.3%)
Neutral or unsure	1037 (47.0%)	48 (26.5%)	668 (34.0%)
Disagree	311 (14.1%)	11 (6.1%)	238 (12.1%)
Strongly disagree	201 (9.1%)	7 (3.9%)	108 (5.5%)

For example, in the above table taken from the Australian Community Survey (and including people who do not attend church), the independent variable is Denomination with which people identify and has been placed in columns. The dependent variable is how positive they feel about church life and is placed in rows. Because the raw numbers of answers are quite different for each denomination, it would be impossible to make comparisons. However, column percentages show that, in total 29.8% of Anglicans are positive about church life (adding the top two rows) compared with 63.6% of Baptists and 48.4% of Catholics. Hence, we can conclude that of the respondents in these three denominations, the Baptists were the most positive about church life.

On the other hand, one may want to look at all the people who are very positive about church life and which denomination they belong to. For that purpose one would need to look at row percentages. In total, there were 565 people who were strongly positive. Of these 34.5% were Anglican, 6.0% were Baptist, and 59.5% were Catholic. Hence, one would conclude that of the respondents to this survey who were very positive about the church, the largest proportion of them were Catholic.

Commonly, the research will want to know whether the differences in numbers do represent a real difference that one could expect to find in the larger population. Assuming that sampling has been random, one can use a chi-squared statistic to give some indication of this. The chi-squared is calculated by looking at the total numbers in each row and total numbers in each column, and from these calculates what would be expected by chance. The difference between the number expected by chance and the actual number is used to build the chi-squared number. Taking into account the total number of cells (which is what the ‘D.F. Figure does in SIMSTAT – degrees of freedom) the significance can be calculated.

A significance figure of .050 means that there are just 50 cases in a 1000 in which such a result would be expected as a result of chance variation. A significance figure of .001 means that only in one case in a thousand would one expect a result such as has been obtained to be a result of chance variation. As a rule of thumb, if the significance figure is higher than .05, it would generally be considered that the evidence was not sufficiently strong to reject the null hypothesis. In other words, there was not sufficient evidence to infer that one would expect that in the wider population from which the sample was drawn that there was a relationship between the two variables one was examining. A figure of less than .010 for significance is preferable, and in some research this would be the ‘cut off’ figure for results considered to be ‘significant’.

One factor which can affect the validity of the chi-squared test is if there many cells in the table with very small numbers. Suppose one included in the above table a group such as the Christadelphians, and one only had a five cases. In that column, the total in the five cells would be only five and some of the cells would probably have no cases in them. As a rule of thumb, the chi-squared test can only be considered to be valid if 5% or less than the total number of cells have less than 5 cases in them.

SIMSTAT offers a range of similar tests of significance which can be used for different types of data. Use ‘Phi’ when one is looking at a table of just two columns and two rows (2 x 2 table). When both variables are ordinal, use Goodman-Krustal’s gamma or Spearman’s Rho to determine significance. Both of these measures vary from +1 to -1 and will indicate the direction of the relationship as well as the strength of the relationship.

SIMSTAT also provides means of graphing the results. While the graphs are of the actual numbers of cases rather than the percentage of cases, they can certainly be helpful in drawing attention to some features of the data. For cross-tabulations it is generally appropriate to choose ‘bar charts’ to illustrate the data. A graph of how positive people feel about attendance and the frequency of attendance makes it very obvious that a large portion of those who never attend are neutral or unsure.

2. Correlation. When the variables are both interval data, a cross-tabulation table will often have far to many cells in it to be able to make sense of the figures. A more appropriate statistic is correlation. In SIMSTAT, correlation can be chosen from the cross-tabulation menu so that under the table, a correlation figure is calculated. However, it is more appropriate to go to Correlation in the Regression sub-menu under statistics. In most cases you can use an X versus Y type of matrix, and a two-tailed test of significance. (Use a one-tailed test of significance if you want to test the idea that the relationship between the two variables is one specific direction, rather than a relationship which could go either way.) Exclude missing values ‘Pairwise’. If you exclude missing values ‘Listwise’ it means that one missing value in a whole range of cases for a particular variable means that no result will be available. If missing values are excluded ‘Pairwise’ it means that if a respondent has filled in a response to one question and not another, just that one’s person’s case will be excluded from the analysis.

SIMSTAT will give a result such as the following:

	Year of Birth
Frequency of church attendance	-.1598*** [-.1809 -.1385]
Frequency of prayer	-.1842*** [-.2052 -.1631]

Probability 2-tails: * – .05 ** – .01 *** – .001.

In the table, above, the Pearson correlation is -.1598 for year of birth and frequency of church attendance and -.1842 for year of birth and prayer. A correlation of 0 means that there is no relationship between the two variables that can be detected. A score of 1 or -1 means that there is a relationship in which for every increase in the one variable, there is a linear increase or decrease in the other variable. In this case, a score of 1 would mean that the higher the ‘Year of Birth’ the higher the frequency of church attendance or prayer, in every case. As a rule of thumb, in sociological research, it would be common to regard correlations of between .1 to .29 as low to moderate; correlations of .3 to .49 as moderate, and anything over .5 as strong. The correlation between year of birth and prayer is a little stronger than the relationship between the year of birth and frequency of church attendance. In both cases there is low to moderate trend: older people tend to attend church more than younger people, and, are even more likely to pray more than younger people.

The negative sign has to do with the direction of the relationship. In this case, year of birth has been used, rather than age. Thus 29 would mean someone was born in 1929 and 60 means someone was born in 1960. The higher the year of birth, the lower the frequencies of church attendance and prayer. Hence, the negative sign in the relationship.

The significance of the relationship is indicated by the number of stars. In this case, three stars indicates that there is only one chance in a thousand that this relationship as has been found in this survey is the product of chance factors. The figures in square brackets give us the 95% confidence interval. We can be 95% confident that the true strength of the relationship in the population from which this sample was drawn would lie between -.1385 and -.1809 for the relationship between year of birth and frequency of church attendance. We can be 95% confident that the strength of the relationship in the population would lie between -.1631 and -.2052 for the relationship between frequency of prayer and year of birth.

One of the limitations of correlation measures is that they are measures of linear relationships and are not sensitive to non-linear relationships. Hence, if the frequency of church attendance was stronger among people in the middle years of life, but equally weak among younger and older people, one would achieve a correlation of 0, even though the non-linear relationship between the two factors was quite strong. To examine non-linear relationships, it is easiest to reduce the interval variable (such as age) to an ordinal variable (or list of age groups) and then examine using cross-tabulation.

3. Comparison of Means. If one variable is interval data and the other variable is ordinal or nominal data, one can use the comparison of means to examine whether there is a relationship. The mean is the measure of the average score of variables for which one has interval data. For each group, one can compare the mean score. For example, is the mean frequency of church attendance (which can be taken as interval data) different for people of different denominations?

In SIMSTAT one may use ‘Breakdown’ to look at the differences – found in the Statistics | Comparisons menu. Having determined that the groups one wants to look at are Anglican, Baptist and Catholic which have been scored 1, 2, and 3 respectively in the data, put in 1 and 3 as the range of X in the ‘Breakdown options’. One may choose detailed statistics for details and a ‘Box and whisker’ plot to illustrate the relationship. The nominal variable would go in the ‘Independent’ list and the interval variable in the ‘Dependent’ list.

SIMSTAT will produce a series of tables of statistics for each of the denominational groups. One can compare mean, median, standard deviation, and other characteristics. The ‘Box and whisker’ plot will illustrate the relationship. The thick horizontal line represents the median (50%) point, and the box represents 50% of all cases. The whiskers represent the range. Any scores found to be more than 1.5 box-lengths from the edge of the box are beyond the ‘whiskers’ and are represented by circles. They are described as ‘outliers’.

If you wish to compare the means of just two groups (say Anglicans and Catholics, or males and females) one can use a T-Test which will provide a comparison of the means and a statistic for the probability that the differences are not a product of chance. The T-Test is very helpful in research in which there are ‘before’ and ‘after’ comparisons to make. Suppose you want to look at the effect of an educational program. You may measure people’s knowledge or attitudes or levels of skill prior to the program, and then again when the program has been completed. The T-Test will provide an indication as to whether the program had a significant impact.

Often one wishes to compare several groups, rather than two. For instance, one may wish to measure whether the frequency of church attendance is significantly different across several denominations. In this case, one would use ONEWAY ANOVA. Apart from providing a list of means for each denomination, the program calculates the extent to which, in each case, the actual score varies from the mean. This calculation is used in the ‘F’ score in Levene’s test of homogeneity. If the probablility or ‘P’ figure is greater than .050, then there is no evidence that the variation in the means is not just the produce of chance. In other words, a probability (P) score of less than .050 means that the differences between the groups is statistically significant.

Tukey’s HSD Multicomparisons test will show where the significant differences lie. It will produce a table of all paired relationships between the groups, a measure of difference, and the significance of the relationship. For example, in examining the relationship between frequency of attendance in the various relationships, using Tukey’s table, one finds that the differences in frequency of attendance between Uniting and Presbyterian people is not significant. Nor is the difference between Orthodox and Catholic significant. However, the differences between Anglican and Uniting and Anglican and Baptist, for example, are significant.

Multivariate AnalysisPlease note: This section is a brief overview of the sorts of multivate analysis that are possible. Its aim is to help in understanding the presentation of multivariate analysis in journal articles and books, and to alert the researcher to what sorts of techniques are possible. We recommend that researchers who wish to rely on these sorts of techniques undertake a course in multivariate analysis, such as those organised annually by the ACSPRI Centre for Social Research (http://acspri.anu.edu.au). There are many books which provide a much more detailed account of the statistical procedures outlined here.Regression AnalysisStatistical programs such as SIMSTAT enable us to go beyond the relationship between two variables and look at multiple relationships between several factors. In the world of people, there are usually a range of factors which have an influence of a particular situation, opinion, or behaviour. One might examine what are the most significant factors, for example, in people becoming involved in voluntary work. Is it true that retired people have more time, and thus become more involved? Or is it the motivational factor that is most important in people becoming involved in voluntary work? It has been argued that church attendance reminds people of their responsibilities and encourages people to be involved in activities which assist others. Churches also provide opportunities for enlisting people in voluntary activities. How important then is church attendance? Again, it has been argued that one of the most important factors is that people believe that they have something to offer. Hence one might expect that people with higher levels of formal education would be likely to be more involved. To look at the relative importance of such a range of factors, one uses REGRESSION. Regression analysis produces a table which indicates the individual significance of a factor while controlling for all the other factors. Regression is an extension of the measures of correlation. Correlation looks at the two variables in the correlation and draws the straight line which best represents the relationship between the two variables. The size of the correlation is the slope of that line, represented by a correlation figure lying between -1 and +1. If you go to the Statistics | Regression | Regression menu, the program will draw a chart like the following:

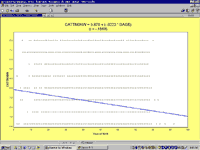
The blue line is the correlation line. It represents the fact that for increases in one’s year of birth, the frequency with what might be expected to attend church decreases. Multiple regression builds on that correlation line and shows how each of the factors included in the regression equation would change its slope. As such, multiple regression looks at ‘linear relationships’ among interval variables. It is possible, however, to include nominal variables in such equations. Variables which are coded as 0 and 1 can be validly treated as interval data and can be entered into a regression. Thus, one could look at the impact of people’s involvement in various denominations, for example, on attendance by creating a series of what are called dummy variables of 0 and 1 from the denomination variable. SIMSTAT actually provides an easy way to do this. In the Data | Transform variable menu there is a ‘Dummy Recoding’ command. It will create a dummy variable for each of the categories in a nominal variable – except for the last category. In using dummy regression, it is necessary to leave out one of the variables for the equation to work. Other variables can also be included in a regression by recoding them as 0s and 1s – such as SEX: 0 for males and 1 for females, for example.It may also be appropriate to include scales developed from several ordinal variables. For example, one could construct a scale of belief by adding together ordinal variables about belief in God, belief in Jesus, belief in the Bible.There are several ways in which regression analysis can include the variables. Suppose one wants to see if the difference between older and younger people in church attendance is due to their overall differences in levels of formal education. One might begin by putting AGE into the equation, and then adding EDUCATION. There is a tab in the SIMSTAT Multiple Regression dialogue box for giving the order of each variable entered into the equation if one chooses the method of regression analysis ‘Hierarchical Selection’. In the results one will look at the overall change in the adjusted R squared. This is an indication of the change in the extent to which education adds to age in explaining the frequency of church attendance. One would also look at the change in the Standardised Beta Coefficient. If the Standardised Beta Coefficient of age in the regression analysis decreases when one adds the factor of education, then one can say that part of the impact of age on church attendance is related to the different levels of formal education among people of different age groups. Another way of doing it is to let the computer work out which independent variable appears to be strongest in relation to the dependent variable. It puts this variable into the equation first, and then adds other variables in order to initial strength. This is the optional method of ‘Forward Selection’. Again, one can look at each step, the changes in the Adjusted R squared, which, in fact, is an indicator of the amount of variation in people’s responses that the equation explains. One can also examine the interplay between the different variables by looking at the changes in the SE Beta – the Standardised Beta Coefficient. Having decided what are the significant independent variables in relation to one’s dependent variable, one can enter them all into the equation using an ‘Enter’ method. This puts all the variables into the equation at the same time. (At this point do not include those variables which appear to add nothing to the equation.) The resulting table from the ‘Enter’ regression is what one would usually present in the journal article or thesis, showing the overall adjusted R square – indicating how much of the variation in the dependent variable one has explained, the Beta and Standardised Beta for each variable, and the level of significance of each variable. (It is possible for a variable to appear to contribute a lot to an equation but for its contribution to be not significant.) For example, here is a regression equation looking at the impact of religion on the levels of satisfaction in life. Model 1 – Dependent Variable ‘Satisfaction in Life’ B (Beta Coefficient) SE B (Standardised Beta Coefficient) Significance Strength of affirmation of Christian beliefs .006 .021 .639 Importance of belief .011 .038 .331 Importance of a spiritual life .040 .050 .275 Importance of having meaning in life .107 .093 .021 Frequency of church attendance .036 .081 .095 Adjusted R square = .009 (indicating that just 0.9% of the variance in the dependent variable is accounted for by the variables in this model).The above variables have little impact on Satisfaction in Life. One variable is significant: the importance of having meaning in life. People who attend church or who affirm Christian beliefs strongly may have slightly higher scores in ‘Satisfaction in Life’ than those people who do not affirm beliefs strongly or attend church, but the differences are not statistically significant, and one cannot assume that one would find those differences in the larger population from which this sample was taken. Model 2 – Dependent Variable ‘Satisfaction in Life’ B (Beta Coefficient) SE B (Standardised Beta Coefficient) Significance Strength of affirmation of Christian beliefs .004 .014 .740 Importance of belief .003 .011 .755 Importance of a spiritual life .002 .030 .949 Importance of having meaning in life .006 .030 .136 Frequency of church attendance .002 .054 .917 Personality – Extrovertism .070 .149 .000 Personality – Neuroticism -.214 -.402 .000 Personality – Psychoticism .050 .061 .000 Adjusted R square = .197 – which means 19.7% of the variation in responses to the question about ‘Satisfaction in life’ is accounted for by the variables in this model.The second model shows that personality variables have a much greater impact on how people report their levels of satisfaction in life than do variables about belief and church attendance. Extrovertism is an important factor. Extroverts generally report that they enjoy life more than do introverts. The most important factor is the level neuroticism in the personality. The fact is some people are ‘worriers’. They are anxious about big and small things in life. Those who are more highly neurotic report lower scores in ‘Satisfaction in Life’. Comparison between the two models shows that when one takes personality factors into account, all of the impact of religious belief disappears. While one could do further regression analysis to see how the various factors of personality have an impact, this regression analysis suggests that attendance at church, for example, is related partly to personality. Other studies have suggested that people who score on psychoticism, which here refers to ‘tender-mindedness’ and sensitivity, tend to have higher levels of church attendance. There are some different forms of regression analysis. There are non-linear forms and also logistic regression analysis which is used when the independent variable is a nominal variable. Discussion of these sophisticated forms of analysis is beyond the scope of this introduction to empirical research. Path Analysis and Structural Equation ModellingPath analysis and structural equation modelling involve the development of models of the relationships of a number of variables. The model is then compared with the data to the strength of the various links between the variables, and how well the model fits the data that one has. A wide range of variables may be included in a model. Structural equation modelling will show the overall strength of the model one has developed and where the model does not fit the data. In general, one will ‘play’ with a model, trying out various ways in which the variables fit together in order to obtain a stronger model. These sorts of techniques are usually found in separate statistical packages. They are not part of SIMSTAT, for example. There is a separate program used with the widely used SPSS statistical program called AMOS. Another well-known and sophisticated program for structural equation modelling is LISREL.Factor AnalysisAnother multivariate technique which is often useful in analysis is factor analysis. Factor analysis has a range of forms, but essentially shows how different variables group together and the strength of the groupings which emerge. For example, in the Australian Community Survey, we asked people about the importance of a total of twenty-two ‘values’ as principles in guiding the respondent’s life. Factor analysis helped us to look at whether these factors grouped together in any particular ways. To help us to ‘separate’ the different factors as much as possible, ‘varimax’ rotation was used. The result was the following table: Values Factor 1 Factor 2 Factor 3 Factor 4 Broad-minded .729 .157 .007 -.004 Creativity .494 .463 -.005 .124 Cleanliness .067 .193 .766 .055 Devout -.043 -.040 .233 .845 Enjoying life .302 .627 .174 -.160 Protecting the environment .690 .078 .187 -.004 Equality .658 .187 -.009 .118 An exciting life .249 .745 -.009 .106 Freedom .596 .305 -.114 .058 True friendship .515 .225 .299 .136 Helpful .567 .005 .303 .336 Honest .617 .006 .444 .147 Meaning in life .383 .367 .129 .485 National security .009 .130 .684 -.021 Politeness .327 .157 .582 .173 Social justice .693 .001 .310 .156 Social recognition .154 .506 .366 .111 A spiritual life .196 .002 -.112 .858 Successful .178 .654 .330 .169 Wealth -.146 .628 .212 -.167 Wisdom .544 .228 .202 .312 World at peace .562 -.003 .405 .028 The factor scores vary from -1 to +1. In interpreting the table, one looks for the highest scores in each factor. These are the most important variables in the factor. For example, in the first column (Factor 1), the highest scores are broadmindedness, social justice, protecting the environment, equality, and honesty. It is apparent, then, that these values tend to be affirmed together. They tend to hang together. The people who are concerned for social justice are also concerned for the environment. Perhaps one could describe this fact as the ‘social concern’ factor. In the second factor, the variables which score highly are: having an exciting life, success, wealth and enjoying life. These suggest that there is a ‘personal pleasure factor’ which dominates the ways some people approach life. The third factor is cleanliness, national security and politeness. It might be described as the ‘social order’ factor. It is interesting to note the negative variables. Those who value social order, place less importance than others on freedom and on a spiritual life, although the small size of these factors means that the negativity associatied with them is not large. The fourth factor is devout and having a spiritual life. Having meaning in life is also relatively strong. This might be described as the ‘spiritual factor’. Another table in the factor analysis results shows the percentage of variance explained. This table indicates how important each factor is in explaining the variation in the scores in the sample. It does not show which factors are of most importance to people overall. Factor Percent of Variance Cumulative Percent 1 31.5 31.5 2 9.0 40.5 3 7.5 48.0 4 6.7 54.7 The table shows that people vary most in relation to Factor 1 – the extent to which they are focussed on social concern, and then secondly on the extent to which their lives are guided by personal pleasure objectives. The four factors, social concern, personal pleasure, social order, and spirituality, together account for 54.7% of the variation in all the scores of these values. We can explain a considerable portion of the variation in values in terms of how people relate to these four life orientations. One way of proceeding from factor analysis is to use this as a guide in the development of scales. One could take the relevant variables and build scales of ‘social concern’, ‘personal pleasure’, ‘social order’ and ‘spirituality’ and then look at whether the people who score high on each of these scales have any particular characteristics. Are those who score ‘personal pleasure’ high, mostly younger people? Are they people who have not had a religious background? Are those who score spirituality high mainly older people who have had a religious background? Factor analysis can be very helpful in identifying patterns in one’s data and, by showing how variables group together, suggest helpful interpretations of the data.There are many forms of factor analysis: principle components analysis (which is what has been explained here), canonical analysis, cluster analysis, and so on. An allied statistical function is discriminant function analysis. For details of these, see texts of statistics.